Zur Bestimmung der Planck-Konstanten mithilfe von LEDs
Auf der Suche nach Experimenten zu dem Lehrstoff Quantenmechanik stößt man als Physiklehrer immer wieder auf "die Bestimmung des planckschen Wirkungsquantums mithilfe von Leuchtdioden". In den betreffenden Versuchsanleitungen wird vorgeschlagen, die kleinste Spannung U zu bestimmen, bei der die Leuchtdiode gerade noch leuchtet. Mit der Frequenz f des ausgesendeten Lichtes soll das plancksche Wirkungsquantum h gemäß der Beziehung
e ⋅ U = h ⋅ f Glg. (1)
bestimmt werden. Hierin gibt e die Elementarladung an. Gleichung (1) wird in den Versuchsanleitungen mit dem Energiesatz begründet. Interessanterweise liefern entsprechende Messungen und Auswertungen von Gleichung (1) stets zu kleine Werte für das plancksche Wirkungsquantum. Oder mit anderen Worten: "Bei den gemessenen Minimalspannungen dürften die Leuchtdioden noch gar nicht leuchten, obwohl sie es tun." Dieser experimentelle Befund kann nun nicht durch Messfehler erklärt werden, sondern zeigt, dass die konsequente Anwendung des Energiesatzes nicht zu Gleichung (1) führt.
Die nachfolgende Abbildung stellt die Energieverhältnisse der Elektronen bei einem p-n-Übergang dar. Die eingezeichnete Diffusionsspannung V (englisch: built-in-voltage) ist eine dem Übergang innewohnende Eigenschaft und kann an den Anschlüssen der Diode nicht gemessen werden. Daher sind konsequenterweise mögliche Einflüsse einer äußeren Spannung in dieser Darstellung nicht berücksichtigt.

In Leuchtdioden rekombinieren Leitungselektronen mit Löchern im Valenzband. Bei einem direkten Übergang wird die frei werdende Energie in Form eines Photons abgegeben. Dies ist in der Abbildung durch einen Übergang in der Sperrschicht von der unteren Kante des Leitungsbandes zur oberen Kante des Valenzbandes kenntlich gemacht. Auffallend an obiger Darstellung ist die völlige Gleichberechtigung der Löcher im p-Leiter mit den Elektronen im n-Leiter. Wenn nun eine äußere Spannung die Energie eines Elektrons um einen bestimmten Betrag ändert, dann muss dieselbe Spannung die Energie eines Loches um denselben Betrag ändern. Oder mit anderen Worten: Da ein Loch im Valenzband einer positiven Ladung entspricht, und das Wort "Rekombination" zumindest zwei Partner impliziert, ist die aufgewendete Energie nicht durch e⋅U sondern durch 2⋅e⋅U gegeben. Diese aufgewendete Energie muss nun für die Überwindung der Diffusionsspannung und der Energie des Photons Sorge tragen. Mithin lässt sich der dem Problem angepasste Energiesatz als
2 ⋅ e ⋅ U = h ⋅ f + e ⋅ V Glg. (2)
anschreiben. Die rechte Seite von Gleichung (2) kann direkt aus der obigen Abbildung abgelesen werden. Wem die Argumentation, die zur linken Seite von Gleichung (2) führte, nicht restlos überzeugt, der möge sich folgende Situation vergegenwärtigen: Ein Elektron werde durch die äußere Spannung von der Kathode zur Anode getrieben. Genauso wandere ein Loch unter dem Einfluss der äußeren Spannung von der Anode zur Kathode. Treffen sie bei der jeweils anderen Elektrode ein, dann sind sie aus dem Kristall verschwunden. Für dieses Verschwinden des Paares ist die Energie 2⋅e⋅U maßgeblich. Wenn nun das gleiche Elektronen-Loch-Paar unter dem Einfluss der äußeren Spannung rekombiniert und daher ebenfalls aus dem Kristall verschwindet, dann sollte diese "Vernichtungsenergie" ebenfalls gleich 2⋅e⋅U sein.
Wenn man bedenkt, dass das Fermi-Niveau in der verbotenen Zone liegt, kommt man zu dem Schluss, dass h⋅f größer als e⋅V ist. Dies führt auf
e ⋅ U < h ⋅ f < 2 ⋅ e ⋅ U
als eine mit dem Experiment verträgliche Ungleichung. Da unterschiedliche Leuchtdioden auch unterschiedliche Diffusionsspannungen aufweisen, kann mit den oben erwähnten Versuchen das plancksche Wirkungsquantum bloß abgeschätzt werden.
Von drei klaren Leuchtdioden der Farben rot, grün und blau wurden die Wellenlängen mittels reellen Gitterbeugungsbildern und die Leuchtspannung, also jene Spannung U an der Diode, bei der das Leuchten mit freiem Auge gerade noch feststellbar ist, bei Raumtemperatur bestimmt. Aus der Wellenlänge lässt sich die Photonenenergie, und damit die Energielücke errechnen. Gemäß Gleichung (2) kann sodann die Diffusionsspannung ermittelt werden. Die relevanten Werte sind in nachstehender Tabelle zusammengefasst.
| LED | Wellenlänge | Photonenenergie | Leuchtspannung | Diffusionsspannung |
| in Nanometer | in Elektronenvolt | in Volt | in Volt | |
| rot | 633 | 1,96 | 1,41 | 0,86 |
| grün | 535 | 2,32 | 1,91 | 1,50 |
| blau | 465 | 2,67 | 2,24 | 1,81 |
Wie zu erwarten war, ist die Leuchtspannung stets größer als die Diffusionsspannung. Dies kann schon als Indiz für die Sinnhaftigkeit von Gleichung (2) gewertet werden.
Obige Ungleichungskette kann verwendet werden, um Schranken für das plancksche Wirkungsquantum zu ermitteln. Da diese Ungleichungskette für alle Leuchtdioden gilt, wird man die größte untere Schranke und die kleinste obere Schranke als Messergebnis angeben:
5,56 ⋅ 10-34 Js < h < 9,52 ⋅ 10-34 Js
Johannes Barton, Wien 2019
Nachtrag: Von zwei anderen Leuchtdioden wurden die Spektren mit einem USB-Spektrometer der Firma "Ocean Optics" bestimmt, wobei eine Serienschaltung der beiden LEDs garantierte, dass durch beide LEDs der gleiche Strom mit einer Stärke von ungefähr 5μA floss.
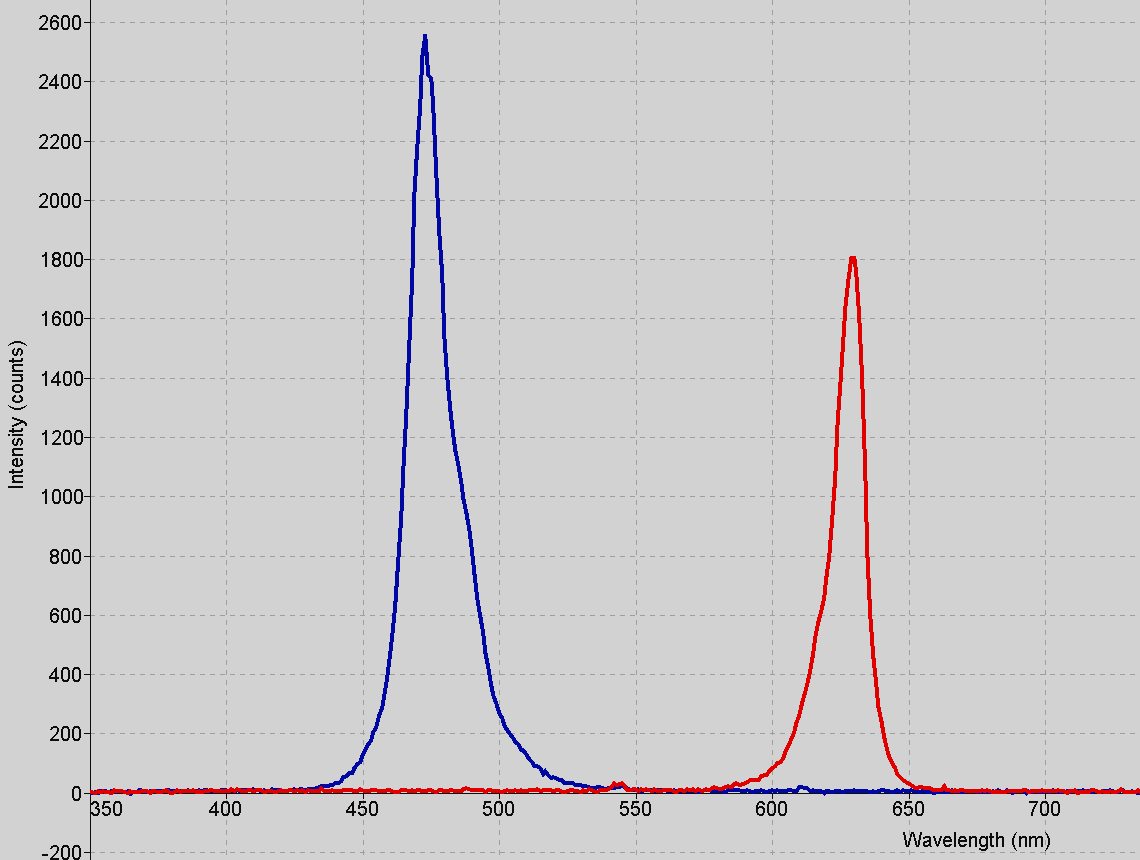
Legt man als Unsicherheit die HWHM zugrunde und vergleicht die auf Elektronenvolt umgerechneten Spektrallinien mit den beobachteten Leuchtspannungen, dann ergibt sich folgendes Ergebnis:
blaue LED: ( 2,62 ± 0,05 ) eV ...... Leuchtspannung = ( 2,25 ± 0,03 ) V
rote LED: ( 1,97 ± 0,03 ) eV ...... Leuchtspannung = ( 1,41 ± 0,01 ) V
Speziell bei der roten LED ist die Diskrepanz zwischen experimentellem Befund und Glg. (1) offensichtlich.
Johannes Barton, Wien 2023
